Firefly and PC GAMESS-related discussion club

Learn how to ask questions correctly

sanya
sanya@photonics.ru

All your problems arise from your poor English. You just misunderstand the messages in the output.

>1. Why this energy on a scale (SCALED BY 1.000)?
>Whether it means, what number 0.280207 is a share of unit? And what then it is taken for unit?
>Really -1311.5429273? Then your algebraic addition does not work.

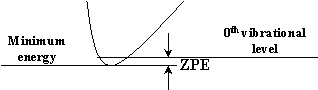
Don't worry about scaling. Dimensionless scaling factor is introduced when you want better agreement of your calculated frequencies with the experiment. In this case you just multiply all your calculated frequencies by a scaling factor (typically, from 0.8 to 1). Since you did not use any scaling, your scaling factor is simply 1. This is what "SCALED BY 1.000" means. Neither frequencies nor ZPE are multiplied by any dimensionless constant and are used "as is", that's it. ZPE is in atomic units, it should be simply added to the final energy (-1311.5429273 au), see the attached picture.

>2. I so understand that those who uses this amendment, spend calculations for ideal gas. So it is
>possible to calculate authors of articles who do it, but article text do not admit. It is a shame
>to them, as their processes go in real, more often water environments. And in the water environment
>as I already have found out practically with use FireFly, differ and very much!
>   Then, if I do PCM-optimise, PCM-tddft, PCM-hessian in the water environment ($PCM solvnt=H2O)
>this ZERO-amendment is not necessary to me?

Anyway, ZPE correction IS necessary (you won't say that the behavior of a quantum oscillator changes in water, will you?). Only thermodynamic functions are calculated in the ideal gas approximation, and only for translational part of these functions. ZPE, which is just a half-sum of all the frequencies, does not depend on the ideal gas. The only approximation used for ZPE is "harmonic oscillator, rigid rotor".

On the other hand, it is not recommended to calculate hessians in PCM because of numerical instabilities and some other computational problems.

Zero-point energy on the potential curve